The Galton Board or Quincunx was developed in order to demonstrate the central limit theorem. It is a simple way to visualize a normal distribution. During the first trimester in my Master’s year for the Simulation module we had this coursework in which we were supposed to create a physics engine in order virtually simulate this experiment. I have choose C++ and OpenGL and I implemented full 3D rigid body motion with friction, angular velocity and speculative contacts (a technique also introduced in Nvidia PhysX 3.4). The biggest challenge of this project was to implement a stable and robust collision detection method which should also be not very computational expensive. I also had to re-familiarize myself with differential calculus in order to better understand the link between mathematics and motion physics.
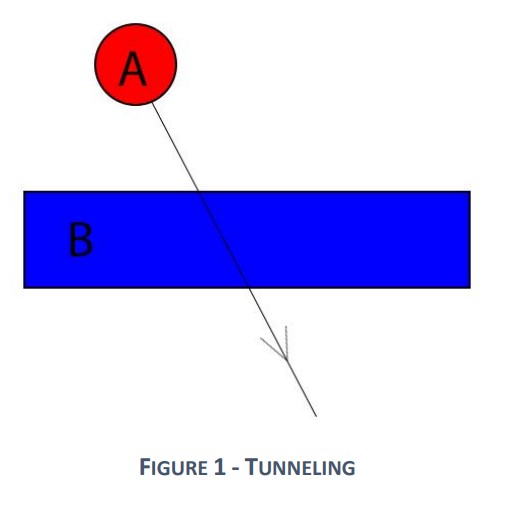
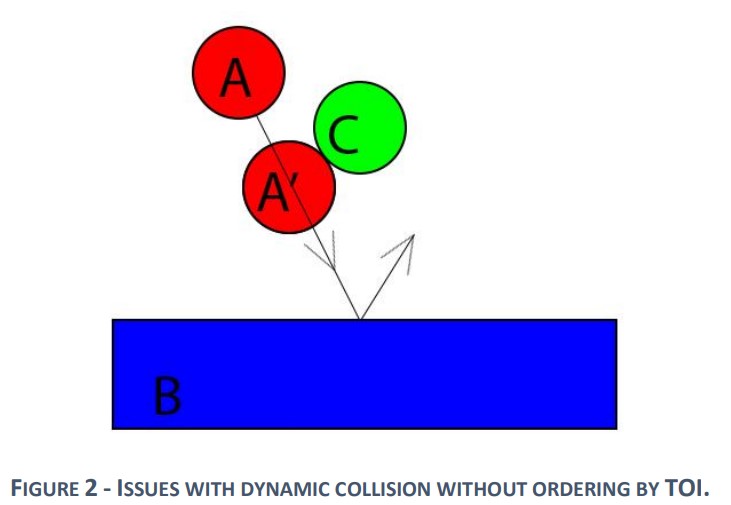
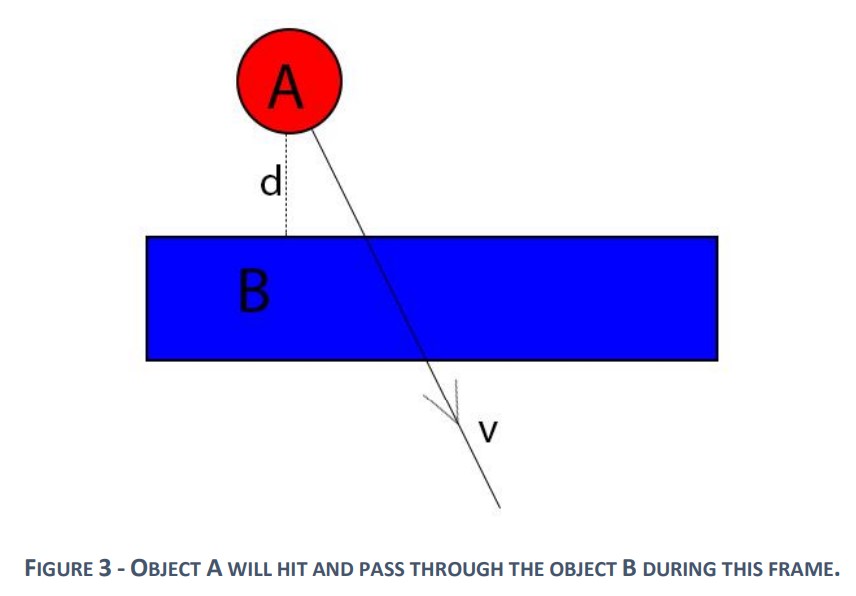
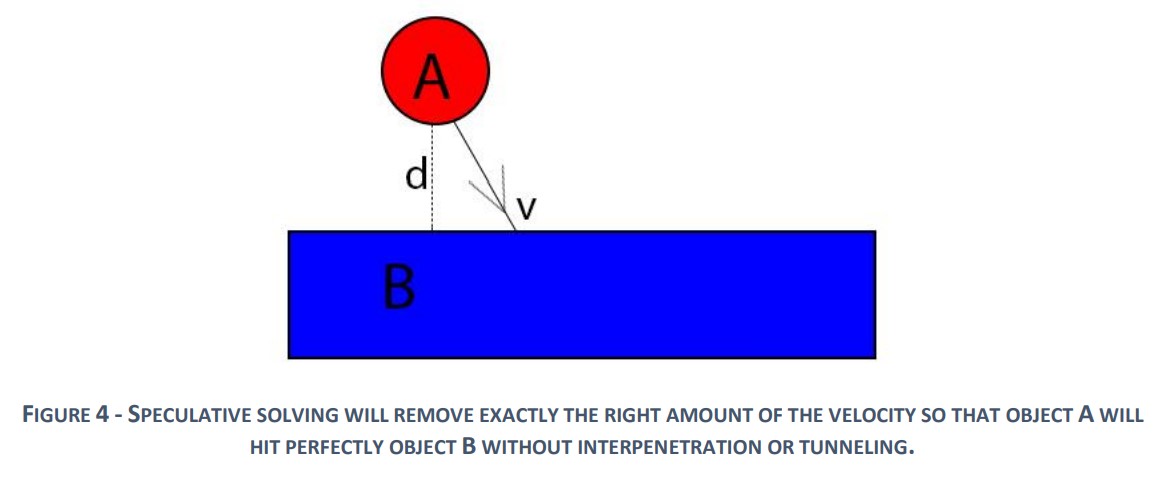
The following section describes the various collision detection methods considered and the advantages of the chosen one.